Enabling Encrypted Delta Compression for Outsourced Storage Systems via Preserving Similarity

通过保留相似性实现外包存储系统的加密增量压缩

摘要：将存储外包到云端可以减轻存储容量的压力，其中加密重复数据删除常用于对加密数据进行重复数据删除，以确保存储效率和安全性。然而，加密重复数据删除只去除重复的加密数据，而没有考虑非重复但非常相似的数据。在本文中，我们提出了 EDelta，这是第一个能够在加密重复数据删除之上，通过保留加密后相似性来实现加密增量压缩，从而进一步减少相似加密数据冗余的方法。我们还提出了两种方法来加速加密增量压缩的加密过程。我们在云环境中原型化了 EDelta，并基于真实世界数据集的实验结果表明，EDelta 可以在加密重复数据删除的基础上实现高达 45.0%的额外数据减少率。

引言

加密重复数据删除可以使用从相同内容中生成的相同密钥对重复的明文块进行加密，这样它们对应的密文块也是相同的，因此可以进行重复数据删除。

尽管重复数据删除加密技术已得到广泛应用，但它只能删除重复的密文块，而不能删除相似的密文块，而相似的密文块在实际存储系统中占很大比例 [12-14]。Delta 增量压缩的补充技术可以在重复数据删除技术之上使用，该技术首先检测数据块的相似性，然后通过存储相似数据块的差异来消除数据冗余，以进一步减少相似数据块的冗余。然而，现有的研究只考虑了在常规重复数据删除之上的增量压缩，而没有考虑加密的重复数据删除。因此，我们提出以下问题：在已经部署了加密重复数据删除的外包存储系统（OSS）中，我们能否继续使用增量压缩以提高存储效率？

发现增量压缩不能直接应用于加密的重复数据删除。主要原因是，由于客户端上的内容不同，两个相似的明文数据块很可能会有完全不同的密钥，因此它们对应的密文数据块也变得完全不同，并在加密后破坏了相似性（详见§II-B），因此无法在云端启用增量压缩。

提出了 EDelta，它可以在加密重复数据删除的基础上实现 delta 增量压缩（称之为加密 delta 增量压缩），其方法是利用基于按位异或的加密重复数据删除操作和基于最大哈希值的密钥来在加密过程中保持相似性。贡献在于：

• 提出了外包存储系统的**加密增量压缩（称为 EDC）**问题

• 提出了 EDelta，它通过基于两个提出的定理来保持相似性，实现了加密的增量压缩，并通过两种提出的方法来提高加密性能

• 实验表明，EDelta 在现有的加密重复数据删除方法基础上，将数据减少率提高了最多 45.0%

背景与挑战

重复数据删除

重复数据删除比传统压缩方法的扩展性更好[16]，特别适用于具有高冗余度的备份/存档应用[17]，而这正是 OSS 典型应用场景。

加密重复数据删除

加密重复数据删除是在加密块上执行重复数据删除，为了提高存储效率和安全性，OSS 对加密重复数据删除进行了广泛研究[6-11]。

基于 MLE 加密去重的的加密过程（如 Convergent Dispersal [20]）：

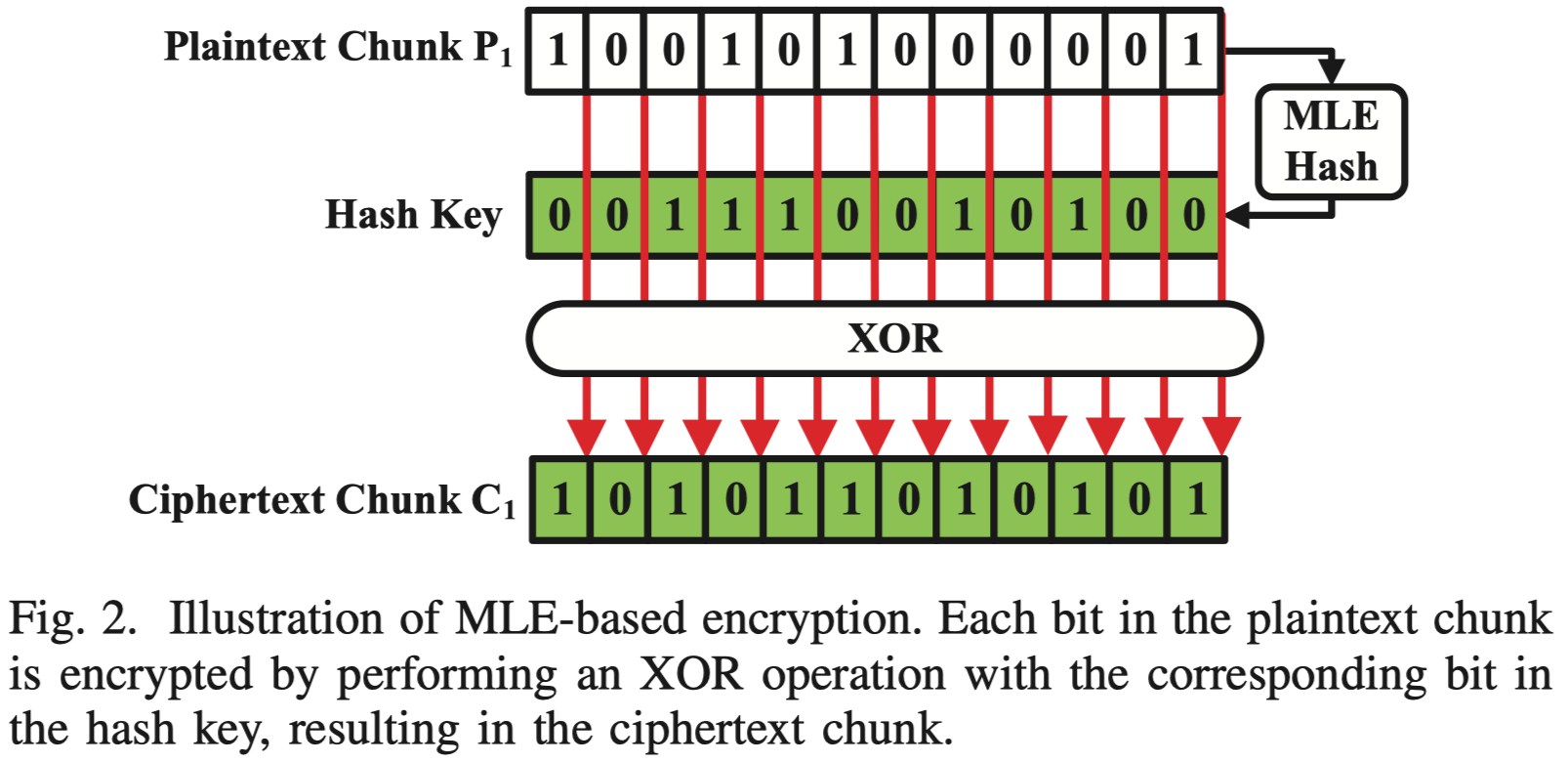
Delta 增量压缩

Delta 增量压缩是备份/归档应用中的另一种流行数据压缩技术【12-14, 21, 22】。它通过消除非重复但高度相似的数据块之间的冗余来实现压缩。

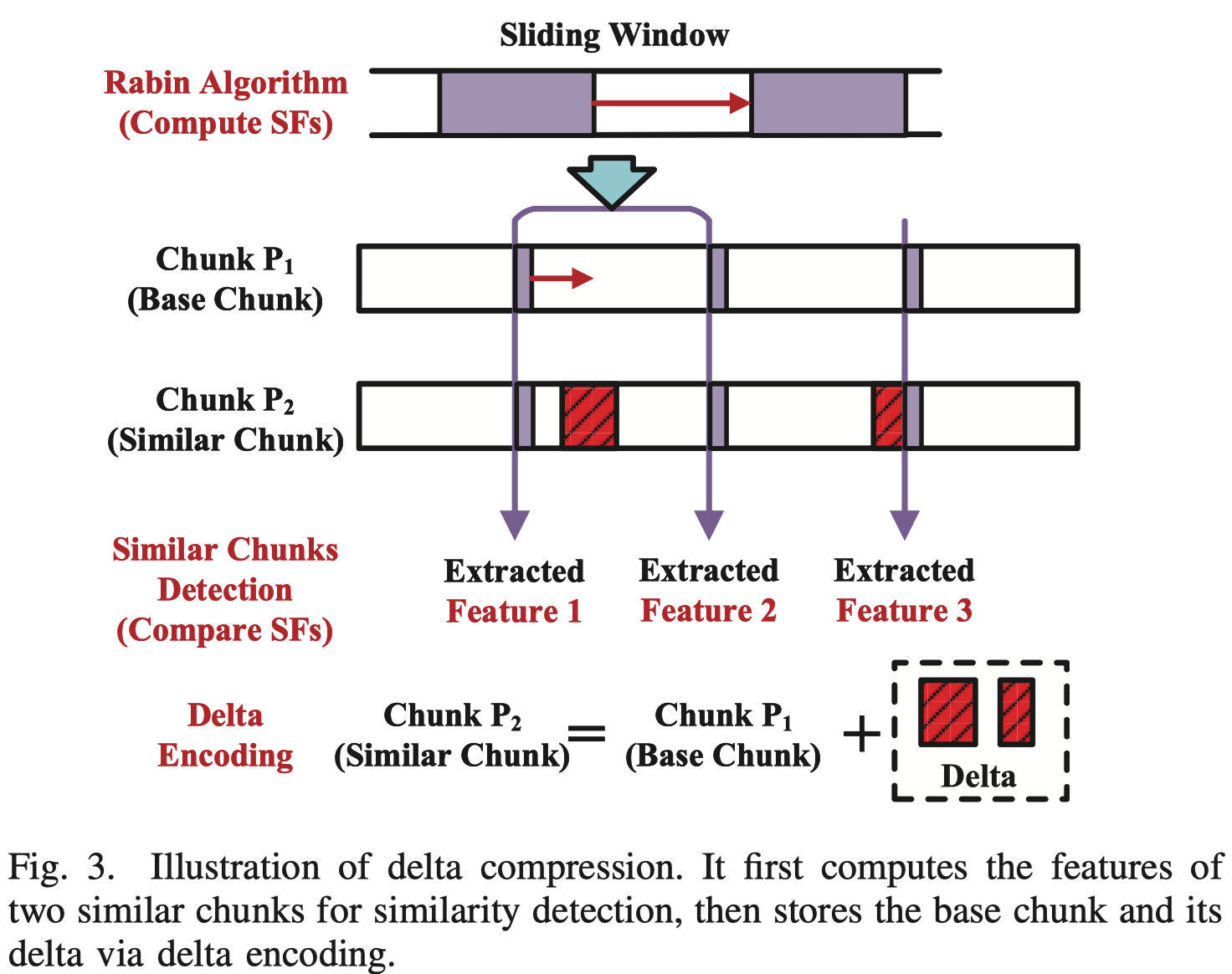
例如，如果两个数据块 P1 和 P2 相似，Delta 压缩只存储 P1（基础块）、它们之间的差异（Δ2,1 = P2 − P1）以及它们之间的映射信息。

对于 Delta 压缩，识别相似数据块的相似性检测是关键步骤。通常基于计算每个数据块的超级特征（super-features，SF）[21, 23, 24]，它由基于 Rabin 指纹计算的多个特征组成。例如，用一个滑动窗口来计算块的特征 $\text{Feature}_i$ 为：

$\text{Feature}_i=\text{Max}_{j=1}^L\left\{\left(m_i \cdot \text {Rabin}_j+a_i\right) \bmod 2^{32}\right\}$

基于 Broder 定理[23, 25]，可以利用数据块的超级特征 SF 来检测高度相似的数据块，该定理暗示了两个集合具有相同最大（或最小）哈希元素的概率与它们的相似度相同[26]。基于这个定理，具有共同的超级特征（即多个特征组成的组）的两个数据块 P1 和 P2 很可能是非常相似的。Delta 增量压缩例子：

挑战

1. 消息锁定加密 MLE 从相似的数据块中生成不同的密钥。
   加密哈希函数表现出雪崩效应，这意味着即使输入数据发生微小变化，例如修改一个比特或字节，都会导致输出哈希值大不相同。因此，相似的明文块将以极高的概率产生两个完全不同的加密哈希值。

2. 按位异或加密使用不相似的密钥会破坏相似性。
   如果两个相似的明文块生成了两个不相似的密钥，那么当前者与后者进行按位异或加密时，相应的密文块显然不相似，这意味着 MLE 加密后相似性未得到保留。

基于上述两个原因，通过在加密后保留相似性来解决实现 EDC 过程中的挑战。

设计

设计了 EDelta 外包存储系统，实现了加密增量压缩（称为 EDC），在加密去重之上进一步减少了冗余，具有以下设计目标：

• 保留相似性，以实现 EDC

  • 证明：如果存在从多个相似的明文块中生成一个相同的哈希密钥，那么相似的明文块会加密成相似的密文块。
  • 证明：相似的明文块很可能具有相同的最大哈希值，这可以作为它们的相同密钥，在 EDC 中保留其相似性。

• 加速 EDC 的加密过程

A. 通过最大哈希密钥保留相似性

主要思想：基于按位异或的加密提供了保持相似块之间相似性的潜力，这意味着如果我们使用相同的哈希值来加密两个相似的块，那么相似明文块的相同部分将在密文块中保持一致，这得益于按位异或的帮助。例如：

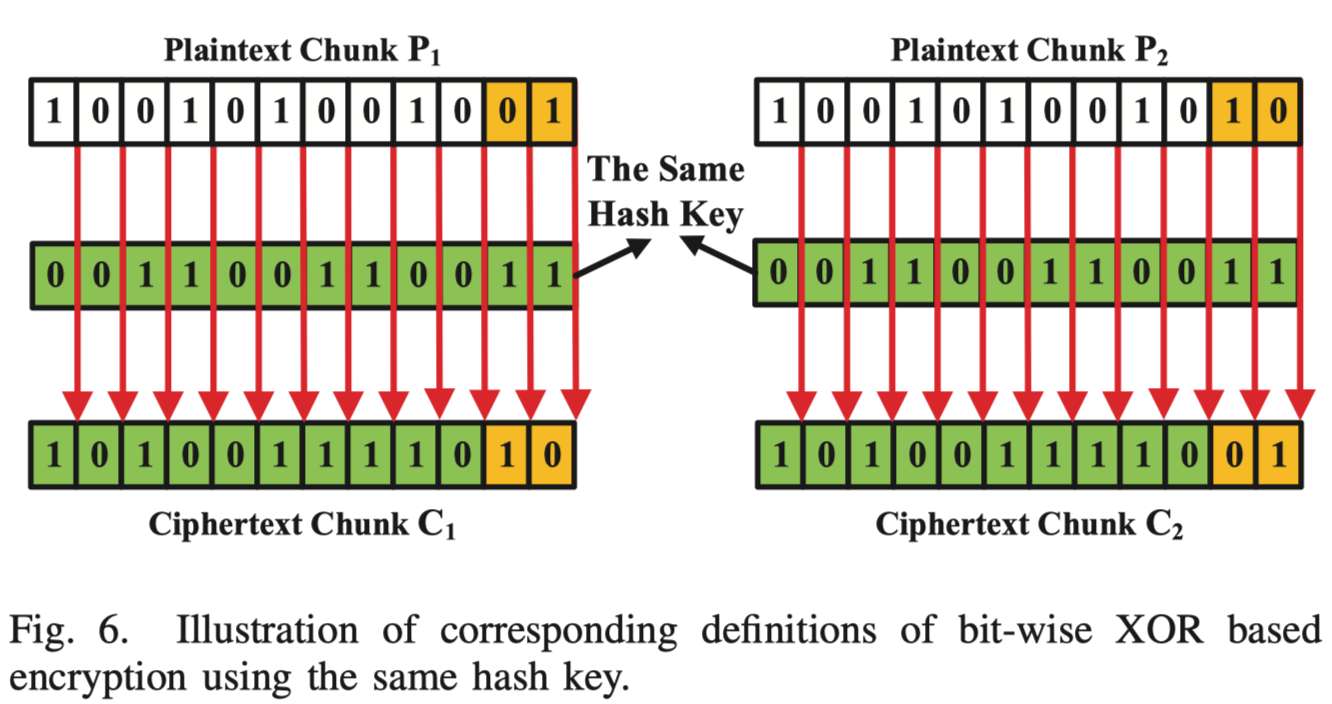
定理 1：通过相同密钥，对相似明文块 $P_1,P_2,\dots, P_n$ 进行按位异或加密得到的密文块 $C_1,C_2, \dots, C_n$ 仍然相似。

定理 1 通过相同密钥加密后可以保持 n 个相似明文块的相似性，从而解决原因 2 带来的挑战。由于原因 1，从 n 个相似块生成相同密钥仍然具有挑战性。

Broder 定理暗示了两个块的相似性与它们的最大哈希值高度相关，这激励我们将 Broder 定理从 2 个相似块扩展到 n 个相似块。自然地问：n（n > 2）个相似块的相似性是否也与它们的最大哈希值高度相关？

定理 2：考虑 $n$ 个集合 $A,B,\dots,N$，其中 $H(A),H(B),\dots,H(N)$ 是分别从 $A,B,\dots,N$ 集合元素生成的哈希值的集合，其中 $H$ 是从一个最小值独立排列族中均匀随机选择的。令 $max(S)$ 表示集合 $S$ 的最大元素。那么：

$\operatorname{Pr}[\max \{H(A) \cup \ldots \cup H(N)\} \in H(A) \cap \ldots \cap H(N)]=\frac{|A \cap \ldots \cap N|}{|A \cup \ldots \cup N|}$